Definizione di Triangolo
Il Triangolo è un poligono formato da tre angoli o vertici e da tre lati.
Classificazione dei Triangoli rispetto ai Lati
Esistono tre differenti tipi di triangoli: isoscele, scaleno ed equilatero.
Triangolo Isoscele
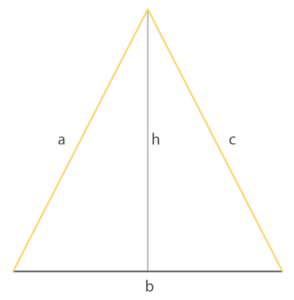
Un triangolo è isoscele se ha due lati congruenti. Gli angoli alla base di un triangolo isoscele sono congruenti.
Triangolo Scaleno
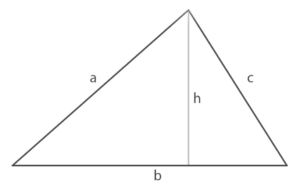
Un triangolo è scaleno se ha i tre lati non congruenti. Gli angoli di un triangolo scaleno non sono congruenti.
Triangolo Equilatero
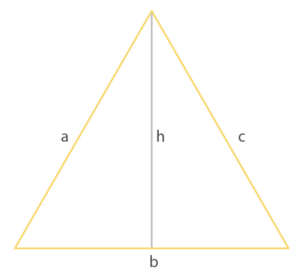
Un triangolo è equilatero se ha i tre lati congruenti. Gli angoli di un triangolo equilatero sono congruenti.
Calcolo dell’Area
$$
A=\frac{b \cdot h}{2}
$$
Formula di Erone
Attraverso la formula di Erone, è possibile calcolare I’area di un triangolo quando sono note le misure dei lati.
In particolare secondo tale formula l’area si ottiene estraendo la radice quadrata dal prodotto del suo semiperimetro per le differenze fra il semiperimetro e ciascuno dei tre lati:
$$
A=\sqrt{\frac{P}{2} \cdot\left(\frac{P}{2}-a\right) \cdot\left(\frac{P}{2}-b\right) \cdot\left(\frac{P}{2}-c\right)}
$$
ponendo $P / 2= p$ (semiperimetro) si ottiene:
$$
A=\sqrt{p \cdot(p-a) \cdot(p-b) \cdot(p-c)}
$$
Calcolo delle Altezze
$$
h_{a}=\frac{2 A}{a}
$$
$$
h_{b}=\frac{2 A}{b}
$$
$$
h_{c}=\frac{2 A}{c}
$$
Mediana
La mediana è il segmento che unisce il vertice con il punto medio del lato opposto.
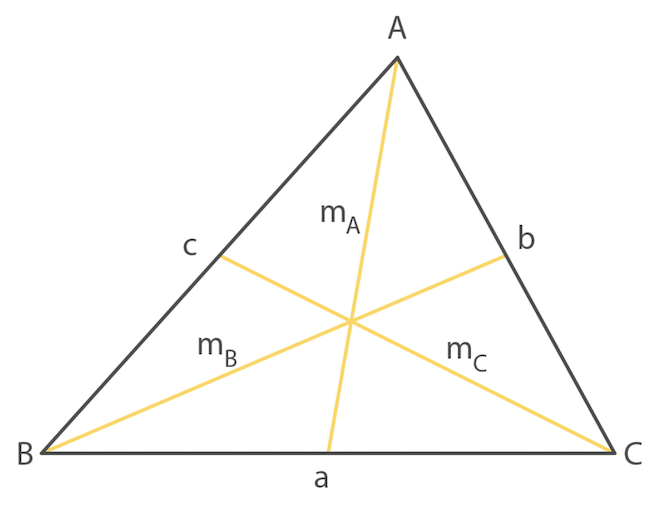
Ciascun triangolo ha tre mediane che si incontrano in un punto detto baricentro (sempre interno a qualsiasi triangolo). Questo punto divide ciascuna mediana in due segmenti l’uno il doppio dell’altro.
Formule per il calcolo della Mediana
Di seguito sono riportate le formule per il calcolo della mediana.
Mediana relativa al vertice $A$
Questa è la formula dela mediana relativa al lato opposto al vertice $A$.
$$
=\frac{1}{2} \sqrt{2\left(A C^{2}+A B^{2}\right)-B C^{2}}
$$
Mediana relativa al vertice $B$
Questa è la formula dela mediana relativa al lato opposto al vertice $B$.
$$
=\frac{1}{2} \sqrt{2\left(B C^{2}+A B^{2}\right)-A C^{2}}
$$
Mediana relativa al vertice C
Questa è la formula dela mediana relativa al lato opposto al vertice $C$.
$$
=\frac{1}{2} \sqrt{2\left(A C^{2}+B C^{2}\right)-A B^{2}}
$$
