Definizione di Trapezio
Il trapezio è un quadrilatero avente solo due lati paralleli.
Esempi svolti
Esempio 1
Il perimetro di un trapezio rettangolo misura
Determinare l’altezza e la proiezione del lato obliquo sulla base maggiore.
Svolgimento
Prima di tutto calcoliamo il lato obliquo DC:
Poi determiniamo il valore dell’altezza
Sostituiamo i valori noti e otteniamo:
A questo punto possiamo calcolare la proiezione del lato obliquo sulla base maggiore come differenza tra le due basi:
Esempio 2
In un trapezio scaleno il perimetro misura
Determinare la lunghezza delle due basi del trapezio.
Svolgimento
Poichè il perimetro è la somma di tutti i lati
possiamo calcolare la somma delle due basi in questo modo:
Sostituendo i valori noti otteniamo:
Ora possiamo calcolare la base minore
A questo punto calcoliamo la base maggiore aggiungendo il valore appena trovato a
Figura Geometrica

Prima Proprietà
I lati paralleli
Seconda Proprietà
I lati non paralleli
Terza Proprietà
La distanza perpendicolare tra le due basi è detta altezza del trapezio, in figura AH e DK.
Quarta Proprietà
I segmenti
Classificazione dei Trapezi
Esistono tre differenti tipi di trapezi: isoscele, rettangolo e scaleno.
Trapezio Isoscele

Nel trapezio isoscele i due lati obliqui e le due diagonali sono uguali.
Inoltre, gli angoli adiacenti a ciascuna base sono uguali e anche le proiezioni dei due lati obliqui
Perimetro Trapezio Isoscele
Area Trapezio Isoscele
Lato Obliquo Trapezio Isoscele
Altezza Trapezio Isoscele
Differenza Basi Trapezio Isoscele
Proiezione Lato Obliquo Trapezio Isoscele
Trapezio Rettangolo
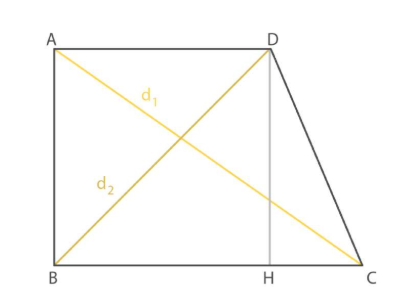
In questa tipologia di trapezio, un lato obliquo è perpendicolare alle due basi
Area Trapezio Rettangolo
Lato Obliquo Trapezio Rettangolo
Altezza Trapezio Rettangolo (con diagonale maggiore e base maggiore)
Altezza Trapezio Rettangolo (con diagonale minore e base minore)
Diagonale Maggiore Trapezio Rettangolo
Diagonale minore Trapezio Rettangolo
Base Maggiore Trapezio Rettangolo
Base Minore Trapezio Rettangolo
Trapezio Scaleno
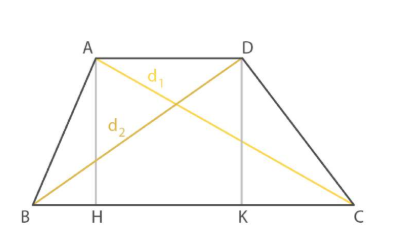
Nel trapezio scaleno i due lati obliqui, le due diagonali e le due proiezioni dei lati obliqui sulla base sono tutti diversi.
Perimetro Trapezio Scaleno
Area Trapezio Scaleno
Base Maggiore Trapezio Scaleno
Base Minore Trapezio Scaleno
Somma delle Basi Trapezio Scaleno
Altezza Trapezio Scaleno
