Definizione di Trapezio
Il trapezio è un quadrilatero avente solo due lati paralleli.
Esempi svolti
Esempio 1
Il perimetro di un trapezio rettangolo misura $44,6 cm$, la base maggiore 18,6 $cm$, la base minore $15 cm$ e il lato non perpendicolare alle basi è $2 / 5$ della base minore.
Determinare l’altezza e la proiezione del lato obliquo sulla base maggiore.
Svolgimento
Prima di tutto calcoliamo il lato obliquo DC:
$$
D C=\frac{2}{5} \cdot 15 $$
$$D C=2 \cdot 3=6 cm
$$
Poi determiniamo il valore dell’altezza $A B$ che è uguale alla differenza tra il perimetro e la somma totale delle due basi e del lato obliquo:
$$
A B=2 p -(A D+B C +D C)
$$
Sostituiamo i valori noti e otteniamo:
$$
A B=44,6-(18,6+15+6) $$
$$A B=44,6-39,6=5 cm
$$
A questo punto possiamo calcolare la proiezione del lato obliquo sulla base maggiore come differenza tra le due basi:
$$
H C=B C-A D $$
$$H C=18,6-15=3,6 cm
$$
Esempio 2
In un trapezio scaleno il perimetro misura $182 cm$, mentre i due lati obliqui misurano $31,5 cm$ e $45,5 cm$. La base maggiore è di $49 cm$ più lunga della base minore.
Determinare la lunghezza delle due basi del trapezio.
Svolgimento
Poichè il perimetro è la somma di tutti i lati
$$
2 p=A D+B C+A B+D C
$$
possiamo calcolare la somma delle due basi in questo modo:
$$
A D+B C=2 p -(A B+D C)
$$
Sostituendo i valori noti otteniamo:
$$
A D+B C=182 -(31,5+45,5) $$
$$A D+B C=182-77
$$
Ora possiamo calcolare la base minore $A D$ in questo modo:
$$
A D =\frac{(A D+B C)-(B C-A D)}{2} $$
$$A D=\frac{105-49}{2}=28 cm
$$
A questo punto calcoliamo la base maggiore aggiungendo il valore appena trovato a $49 cm$ :
$$
B C=A D+49 $$
$$B C=28+49=77 cm
$$
Figura Geometrica

Prima Proprietà
I lati paralleli $AD$ e $BC$ si dicono rispettivamente base minore e base maggiore del trapezio.
Seconda Proprietà
I lati non paralleli $A B$ e $C D$ si dicono lati obliqui del trapezio.
Terza Proprietà
La distanza perpendicolare tra le due basi è detta altezza del trapezio, in figura AH e DK.
Quarta Proprietà
I segmenti $BH$ e KC sono chiamati proiezioni dei lati obliqui sulla base maggiore.
Classificazione dei Trapezi
Esistono tre differenti tipi di trapezi: isoscele, rettangolo e scaleno.
Trapezio Isoscele

Nel trapezio isoscele i due lati obliqui e le due diagonali sono uguali.
Inoltre, gli angoli adiacenti a ciascuna base sono uguali e anche le proiezioni dei due lati obliqui $BH$ e KC.
Perimetro Trapezio Isoscele
$$
2 p=A D+B C+2 A B
$$
Area Trapezio Isoscele
$$
A=\frac{(A D+B C)}{2} \cdot A H
$$
Lato Obliquo Trapezio Isoscele
$$
=\sqrt{A H^2+[(B C-A D) / 2]^2}
$$
Altezza Trapezio Isoscele
$$
=\sqrt{A B^2-[(B C-A D) / 2]^2}
$$
Differenza Basi Trapezio Isoscele
$$
\begin{array}{c}
B C-A D=2 \
\cdot \sqrt{A B^2-A H^2}
\end{array}
$$
Proiezione Lato Obliquo Trapezio Isoscele
$$
\frac{B C-A D}{2}=\sqrt{A B^2-A H^2}
$$
Trapezio Rettangolo
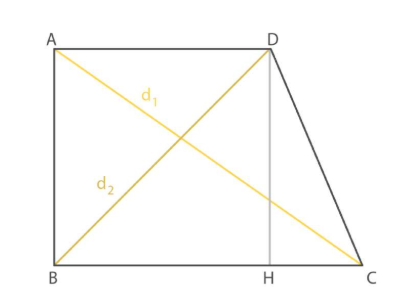
In questa tipologia di trapezio, un lato obliquo è perpendicolare alle due basi $e$ le due diagonali sono diverse. II trapezio rettangolo ha solo una proiezione del lato obliquo $HC$.
Area Trapezio Rettangolo
$$
A=\frac{(A D+B C)}{2} \cdot A H
$$
Lato Obliquo Trapezio Rettangolo
$$
D C=\sqrt{A B^2+(B C-A D)^2}
$$
Altezza Trapezio Rettangolo (con diagonale maggiore e base maggiore)
$$
A B=\sqrt{A C^2-B C^2}
$$
Altezza Trapezio Rettangolo (con diagonale minore e base minore)
$$
A B=\sqrt{B D^2-A D^2}
$$
Diagonale Maggiore Trapezio Rettangolo
$$
A C=\sqrt{B C^2+A B^2}
$$
Diagonale minore Trapezio Rettangolo
$$
B D=\sqrt{A D^2+A B^2}
$$
Base Maggiore Trapezio Rettangolo
$$
B C=\sqrt{A C^2-A B^2}
$$
Base Minore Trapezio Rettangolo
$$
A D=\sqrt{B D^2-A B^2}
$$
Trapezio Scaleno
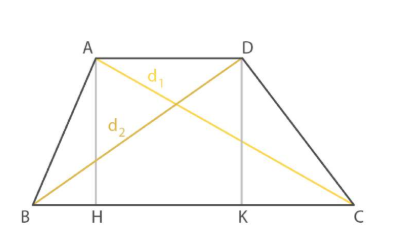
Nel trapezio scaleno i due lati obliqui, le due diagonali e le due proiezioni dei lati obliqui sulla base sono tutti diversi.
Perimetro Trapezio Scaleno
$$
2 p=A D+B C+A B+D C
$$
Area Trapezio Scaleno
$$
A=\frac{(A D+B C)}{2} \cdot A H
$$
Base Maggiore Trapezio Scaleno
$$
B C=\frac{2 A}{A H}-A D
$$
Base Minore Trapezio Scaleno
$$
A D=\frac{2 A}{A H}-B C
$$
Somma delle Basi Trapezio Scaleno
$$
A D+B C=\frac{2 A}{A H}
$$
Altezza Trapezio Scaleno
$$
A H=\frac{2 A}{A D+B C}
$$
