Enunciato del Teorema di Addizione delle Probabilità
La probabibilità che si verifichi almeno uno dei due eventi A e B è pari alla somma delle probabilità dei singoli eventi, meno la probabilità che si verifichino contemporaneamente. In formule:
$$
\begin{gathered}
P(A \cup B)=P(A)+P(B) \
-P(A \cap B)
\end{gathered}
$$
Spiegazione
La formula del teorema di addizione delle probabilità equivale a:
$$
\begin{gathered}
P(A+B)=P(A)+P(B) \
-P(A \cdot B)
\end{gathered}
$$
Questa regola vale soltanto se gli eventi sono compatibili.
Osserviamo la figura
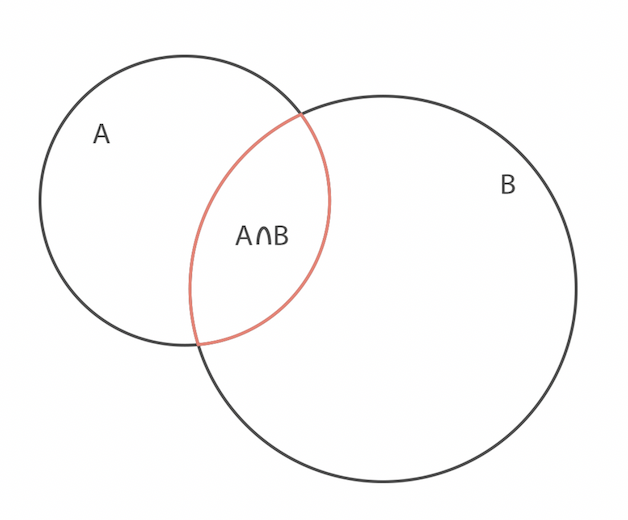
Se i due insiemi rappresentano rispettivamente la probabilità di successo dell’evento $A$ e dell’evento $B$, allora la probabilità che si verifichi almeno uno dei due è uguale alla somma delle aree dei due insiemi.
Quando consideriamo l’unione dei due insiemi è necessario eliminare la quantità relativa alla loro intersezione poichè questa viene considerata due volte: una volta per ciascun insieme.
Esempi svolti
Un’urna contiene 30 palline: 10 rosse numerate da 1 a 10, 10 blu e 10 nere numerate allo stesso modo. Determinare la probabilità che, estraendo una pallina a caso, venga estratta una pallina blu o dispari.
Svolgimento
II numero di palline totali è 30 . La probabilità che venga estratta una pallina blu è:
$$
P(A)=\frac{10}{30}=\frac{1}{3}
$$
Le palline con numero dispari sono 5 per ciascun colore, quindi 15. La probabilità che venga estratto un numero dispari è:
$$
P(B)=\frac{15}{30}=\frac{1}{2}
$$
Gli eventi risultano essere compatibili. I casi favorevoli a entrambi gli eventi sono 5 (pallina blu e dispari).
Gli eventi risultano essere compatibili. I casi favorevoli a entrambi gli eventi sono 5 (pallina blu e dispari).
Pertanto la probabilità dell’evento cercato è dato dall’applicazione della formula del teorema di addizione delle probabilità:
$$
\begin{aligned}
P(A \cup B) & =\frac{1}{3}+\frac{1}{2}-\frac{5}{30} \
& =\frac{2}{3}
\end{aligned}
$$
