Enunciato del Teorema dei Seni
In un triangolo qualsiasi il rapporto tra un lato ed il seno dell’angolo opposto è costante ed è uguale al diametro
Esempi svolti
Calcolare la misura del lato
Svolgimento
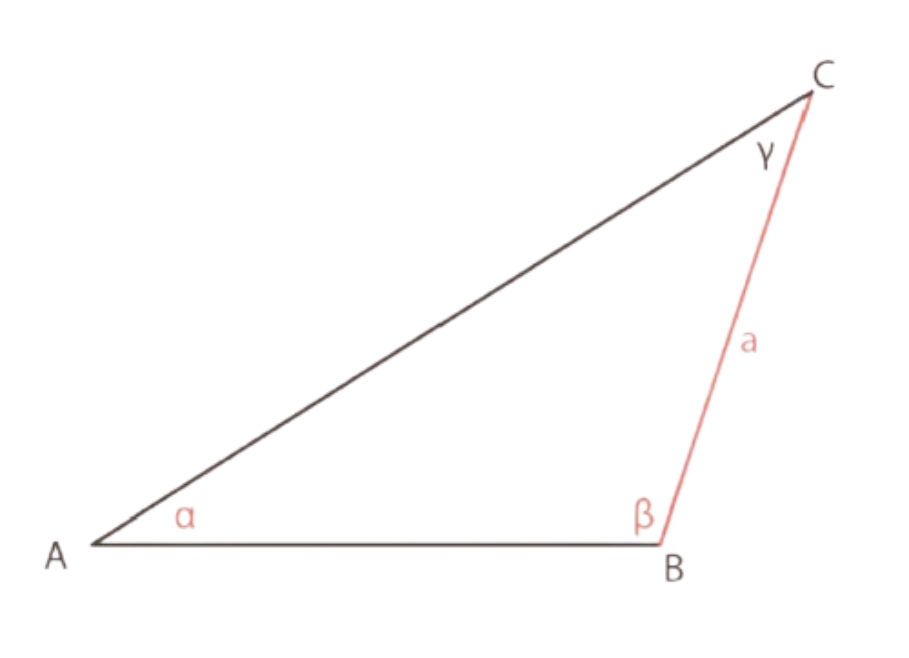
Per applicare il teorema dei seni, occorre determinare l’ampiezza dell’angolo
Sappiamo che la somma degli angoli interni di un triangolo è
Applichiamo la relazione
Sostituiamo i valori del problema:
Il lato c sarà:
Spiegazione del Teorema
॥ Teorema dei Seni può essere espresso in formule nel seguente modo:
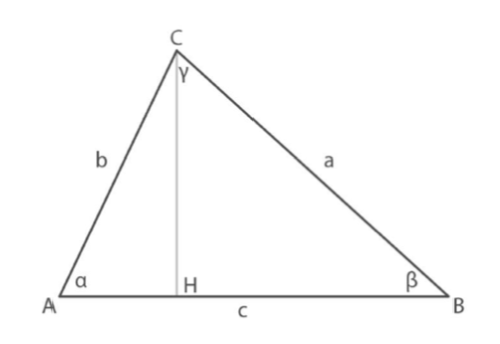
Considerando l’altezza
L’altezza
Mentre per il triangolo rettangolo a destra, l’altezza h è uguale a:
Uguagliando le due espressioni otteniamo:
da cui deriva la tesi del teorema.
