Enunciato del Teorema dei Seni
In un triangolo qualsiasi il rapporto tra un lato ed il seno dell’angolo opposto è costante ed è uguale al diametro $2 r$ della circonferenza circoscritta al triangolo.
Esempi svolti
Calcolare la misura del lato $A B$ del triangolo $A B C$ sapendo che $\alpha=30^{\circ}, \beta=$ $105^{\circ}$ e che la misura del lato $B C$ è $12 \mathrm{~cm}$.
Svolgimento
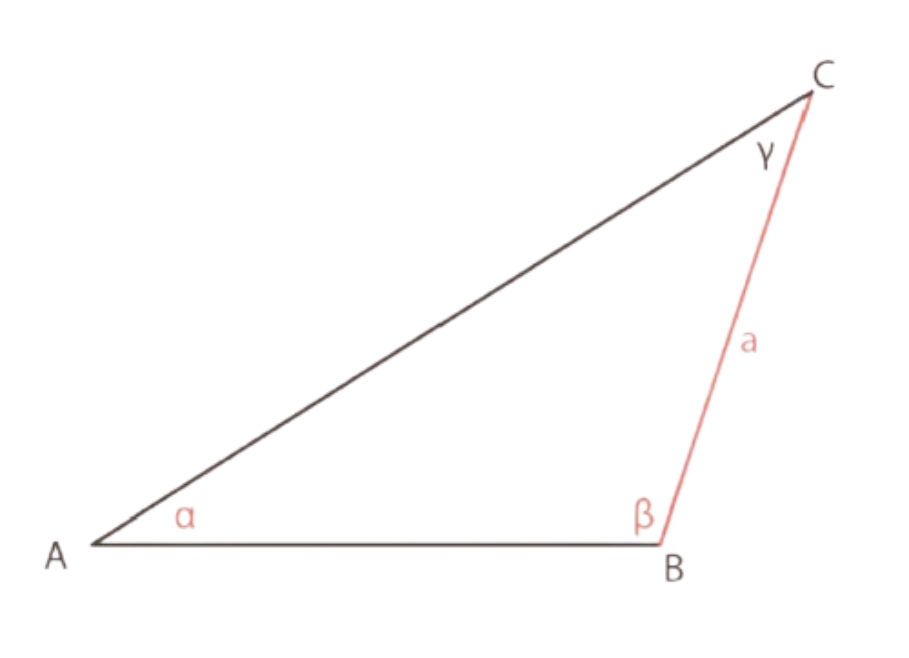
Per applicare il teorema dei seni, occorre determinare l’ampiezza dell’angolo $\gamma$.
Sappiamo che la somma degli angoli interni di un triangolo è $180^{\circ}$, quindi I’angolo $\gamma$ si calcola in questo modo:
$$
\gamma=180^{\circ}-\left(30^{\circ}+105^{\circ}\right) $$
$$\gamma=45^{\circ}
$$
Applichiamo la relazione
$$
\frac{a}{\sin \alpha}=\frac{c}{\sin \gamma}
$$
Sostituiamo i valori del problema:
$$
\frac{12}{\sin 30^{\circ}}=\frac{c}{\sin 45^{\circ}} $$
$$\frac{12}{\frac{1}{2}}=\frac{c}{\frac{\sqrt{2}}{2}}
$$
Il lato c sarà:
$$
c=\frac{12 \cdot \frac{\sqrt{2}}{2}}{\frac{1}{2}} $$
$$c=6 \sqrt{2} \cdot 2 $$
$$c=12 \sqrt{2} \mathrm{~cm}
$$
Spiegazione del Teorema
॥ Teorema dei Seni può essere espresso in formule nel seguente modo:
$$
\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}
$$
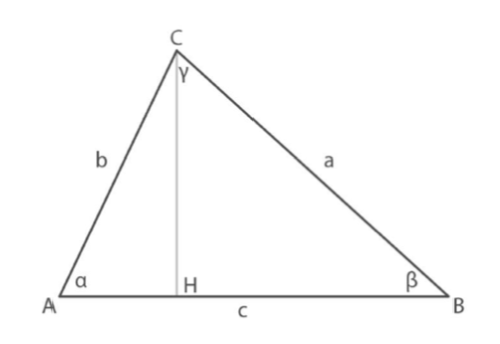
Considerando l’altezza $\mathbf{h}$ mostrata in figura, si può vedere che il triangolo viene diviso in due triangoli rettangoli $\mathrm{ACH}$ e $\mathrm{BCH}$, entrambi retti in $\mathrm{H}$.
L’altezza $h$ può essere calcolata utilizzando il primo teorema dei triangoli rettangoli, quindi avremo che nel triangolo rettangolo a sinistra, l’altezza $\mathbf{h}$ è:
$$
h=b \cdot \sin \alpha
$$
Mentre per il triangolo rettangolo a destra, l’altezza h è uguale a:
$$
h=a \cdot \sin \beta
$$
Uguagliando le due espressioni otteniamo:
$$
b \cdot \sin \alpha=a \cdot \sin \beta
$$
da cui deriva la tesi del teorema.
