Definizione di Rombo
Il rombo è un parallelogramma con i lati congruenti.
Esempi svolti
Determinare la misura della diagonale maggiore di un rombo, sapendo che l’area misura $504,4 \mathrm{~m}^2$ e che la sua diagonale minore è lunga $11,9 \mathrm{~m}$.
Svolgimento
Per calcolare la diagonale maggiore del rombo occorre semplicemente utilizzare la formula:
$$
d_1=\frac{2 \cdot A}{d_2}
$$
Pertanto, sostituendo i valori noti otteniamo la misura della diagonale maggiore:
$$
d_1=\frac{2 \cdot 304,4}{19,1} $$
$$d_1=\frac{608,8}{19,1}=31,87 m
$$
Prima Proprietà
Le diagonali del rombo sono perpendicolari.
Seconda Proprietà
Ciascuna diagonale divide il rombo in due triangoli isosceli.
Terza Proprietà
Gli angoli opposti sono congruenti.
Figura Geometrica
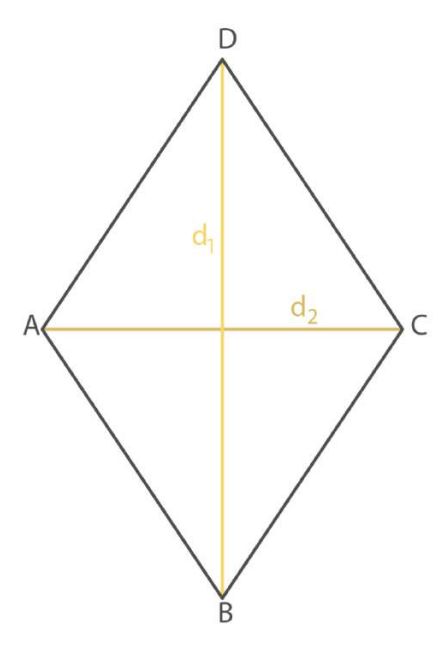
Perimetro
$$
2 p=A B \cdot 4
$$
Area
$$
A=\frac{d_1 \cdot d_2}{2}
$$
Diagonale Maggiore
$$
d_1=\frac{2 \cdot A}{d_2}
$$
Diagonale Minore
$$
d_2=\frac{2 \cdot A}{d_1}
$$
Lato del Rombo
$$
A B=\sqrt{\left(\frac{d_1}{2}\right)^2+\left(\frac{d_2}{2}\right)^2}
$$
