Definizione di Quadrilatero
Il Quadrilatero è un poligono di quattro lati avente quindi quattro vertici e quattro angoli interni.
Figura geometrica
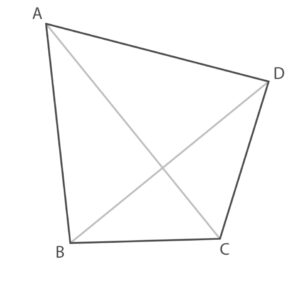
Condizione di Inscrittiibilità
Un quadrilatero è inscrivibile in una circonferenza se le somme delle ampiezze degli angoli opposti coincidono.
$$
\hat{A}+\hat{C}=\hat{B}+\hat{D^{\hat{n}}}
$$
Condizione di Circoscittibilità
Un quadrilatero può essere circoscritto ad una circonferenza se le somme delle misure delle coppie di lati opposti coincidono.
$$
A D+B C=A B+D C
$$
Teorema di Tolomeo
II prodotto delle misure delle diagonali è uguale alla somma dei prodotti delle misure delle due coppie di lati opposti del quadrilatero. Vale soltanto per i quadrilateri inscrivibili in una circonferenza.
$$
A C \cdot B D=A B \cdot D C+A D \cdot B C
$$
Teorema di Legendre
In un quadrilatero convesso inscritto in una circonferenza il rapporto delle diagonali è uguale al rapporto delle somme dei prodotti dei lati che
concorrono negli estremi delle rispettive diagonali.
$$
\frac{A C}{B D}=\frac{A B \cdot B C+A D \cdot D C}{A B \cdot A D+B C \cdot D C}
$$
Formula di Brahmagupta
La formula di Brahmagupta consente di determinare I’area di un quadrilatero inscrivibile in una circonferenza, note le lunghezze dei lati.
$$
=\sqrt{(p-a)(p-b)(p-c)(p-d)}
$$
dove $p$ è il semiperimetro.
