Definizione di Quadrato
Il quadrato è un parallelogramma che ha tutti i lati congruenti e tutti gli angoli congruenti.
Esempi svolti
Determinare le misure della diagonale e del perimetro di una quadrato, la cui area misura $256 m ^2$.
Svolgimento
Attraverso la formula
$$
A B=\sqrt{A}
$$
è possibile calcolare il lato del quadrato.
$$
A B=\sqrt{256}=16 m
$$
A questo punto possiamo determinare la diagonale del quadrato utilizzando la formula
$$
d=\sqrt{2 \cdot A B^2}
$$
Quindi sostituiamo i valori noti e abbiamo:
$$
\begin{array}{r}
d=\sqrt{2 \cdot 16^2}=\sqrt{512} \
d=22,62 m
\end{array}
$$
Il perimetro è uguale al prodotto del lato per 4:
$$
2 p=16 \cdot 4=64 m
$$
Prima Proprietà
Le diagonali del quadrato sono congruenti.
Seconda Proprietà
Le diagonali del quadrato sono perpendicolari e dividono gli angoli a metà.
Terza Proprietà
I lati opposti sono paralleli.
Figura Geometrica
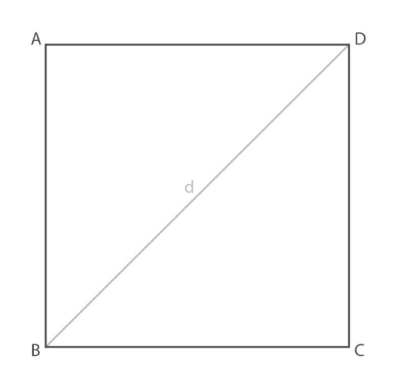
L’area è uguale al lato $A B$ al quadrato.
$$
A=A B^2
$$
Perimetro
Il perimetro è uguale a quattro volte il lato $A B$.
$$
2 p=A B \cdot 4
$$
Diagonale
La diagonale è uguale alla radice quadrata del lato al quadrato $A B$ per 2 .
$$
d=\sqrt{2 \cdot A B^2}
$$
Lato
Il lato è uguale alla radice quadrata dell’area.
$$
A B=\sqrt{A}
$$
