Definizione di Parallelogramma
Un parallelogramma è un quadrilatero con i lati opposti paralleli.
Esempi svolti
Determinare la lunghezza dei lati di un parallelogramma sapendo che il perimetro misura $152 \mathrm{~cm}$ e che due lati consecutivi sono tali che il primo è $17 \mathrm{~cm}$ inferiore del doppio dell’altro.
Svolgimento
La prima cosa da fare è scrivere sotto forma di equazione la misura dei lati. Quindi abbiamo che il lato AD è 2 volte il lato consecutivo DC meno 17:
$$
A D=2 D C-17
$$
Sappiamo che il perimetro del parallelogramma è la somma dei lati e poichè i lati sono a due a due congruenti possiamo scrivere che:
$$2 p=2 A D+2 D C
$$
Sostituendo i dati si ottiene:
$$ 152=2 \cdot (2 D C-17)+2 D C$$
Risolvendo l’equazione in incognita $DC$ si ha:
$$ 152= 4 DC – 34 + 2 DC$$
$$ 152=6 DC – 34$$
$$ 6 DC= 152+34$$
$$ 6 DC=186$$
$$ DC= \frac{186}{6}= 31\mathrm{~cm}$$
Andiamo a sostituire al lato AD la sua espressione in funzione dell’altro lato:
$$A D=2 D C-17= 2 \cdot 31 – 17=62-17=45 \mathrm{~cm}$$
I lati del parallelogramma misurano $31 \mathrm{~cm}$ e $45 \mathrm{~cm}$ .
Prima Proprietà
In un parallelogramma ciascuna diagonale lo divide in due triangoli congruenti.
Seconda Proprietà
In un parallelogramma i lati opposti sono congruenti.
Terza Proprietà
Gli angoli opposti sono congruenti tra loro.
Quarta Proprietà
Gli angoli adiacenti a ogni lato sono supplementari.
Quinta Proprietà
Nei parallelogrammi le diagonali si incontrano nel loro punto medio.
Formule del Parallelogramma
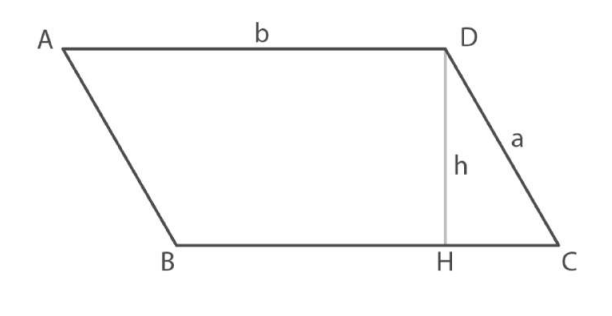
Perimetro
$$
2 p=2 a+2 b
$$
Base
$$
b=\frac{2 p-2 a}{2}
$$
Lato Obliquo
$$
a=\frac{2 p-2 b}{2}
$$
Area
$$
A=b \cdot h
$$
Base nota l’Area
$$
b=\frac{A}{h}
$$
Altezza
$$
h=\frac{A}{b}
$$
