Definizione di Numero Complesso
I numeri complessi sono espressioni matematiche della forma a $+i b$, dove a e b rappresentano due numeri reali e $i$ rappresenta l’unità immaginaria.
Esempi svolti
Esempio 1
Semplificare la seguente espressione
$$
(\sqrt{2}-i)-i(1-\sqrt{2 i})
$$
$$
\begin{array}{l}
=\sqrt{2}-i-i+\sqrt{2 i^2}= \
=\sqrt{2}-2 i-\sqrt{2}=-2 i
\end{array}
$$
Esempio 2
$$
\begin{array}{c}
(3+i)(3-i)\left(\frac{1}{5}+\frac{1}{10} i\right)= \
=\left(9-i^2\right) \cdot \frac{2+i}{10}= \
=(9+1) \cdot \frac{2+i}{10}=2+i
\end{array}
$$
Unità immaginaria
$$
i=\sqrt{-1}
$$
Addizione e Sottrazione
L’addizione con i numeri immaginari equivale a:
$$
a i+b i=(a+b) i
$$
L’addizione gode delle proprietà commutativa, associativa, esistenza dell’elemento neutro (zero) e esistenza dell’opposto.
Mentre la sottrazione è:
$$
a i-b i=(a-b) i
$$
Moltiplicazione e Divisione
La moltiplicazione o la divisione di un numero immaginario per un numero reale è un numero immaginario.
$$
a i \cdot b=b \cdot a i=(a b) \cdot i
$$
$$
a i: b=(a: b) i \quad b \neq 0
$$
Moltiplicazione e Divisione di due numeri immaginari
Il prodotto o il quoziente di due numeri immaginari è un numero reale.
$$
\begin{array}{r}
a i \cdot b i=a \cdot b \cdot i^2 \
=a \cdot b(-1) \
=-a b
\end{array}
$$
$$
a i:(b i)=a: b
$$
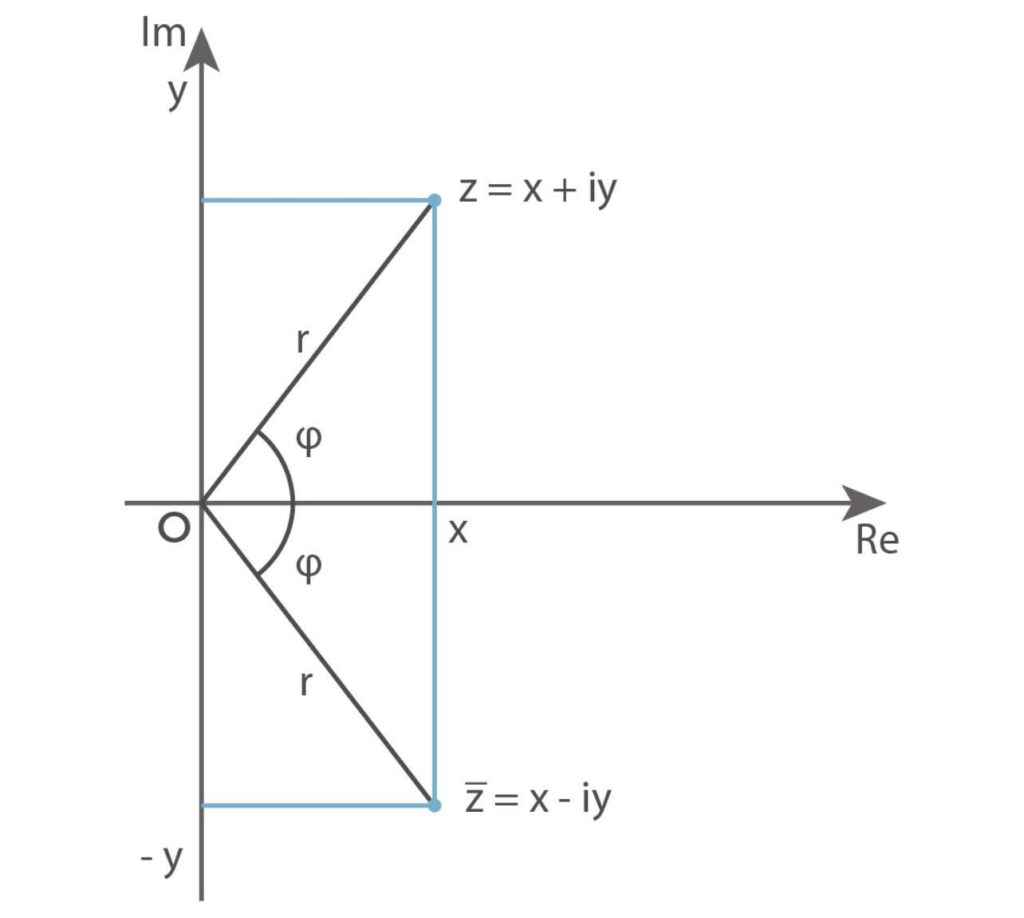
Rappresentazione sul Piano Cartesiano
Un numero complesso può essere visto come un punto del piano cartesiano. Una rappresentazione di questo tipo si chiama diagramma di Argand.