Definizione di insieme
In matematica si usa la parola insieme per indicare una collezione di oggetti che sono detti elementi dell’insieme e che sono ben definiti e distinti tra loro.
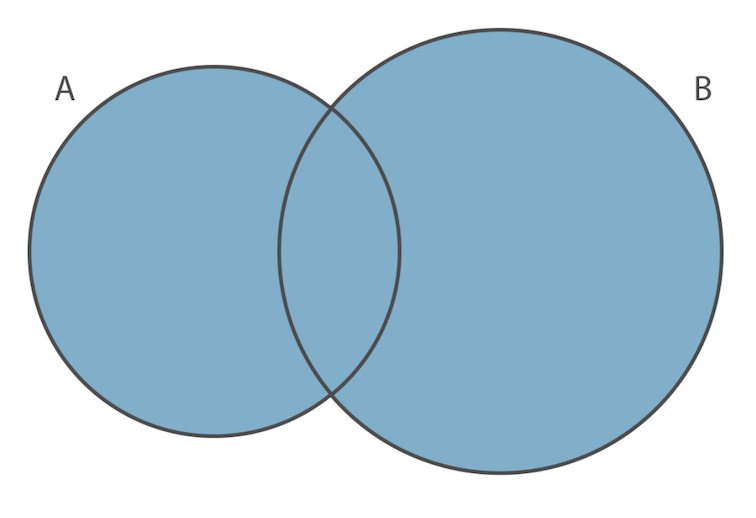
Unione di Insiemi
L’unione di due insiemi
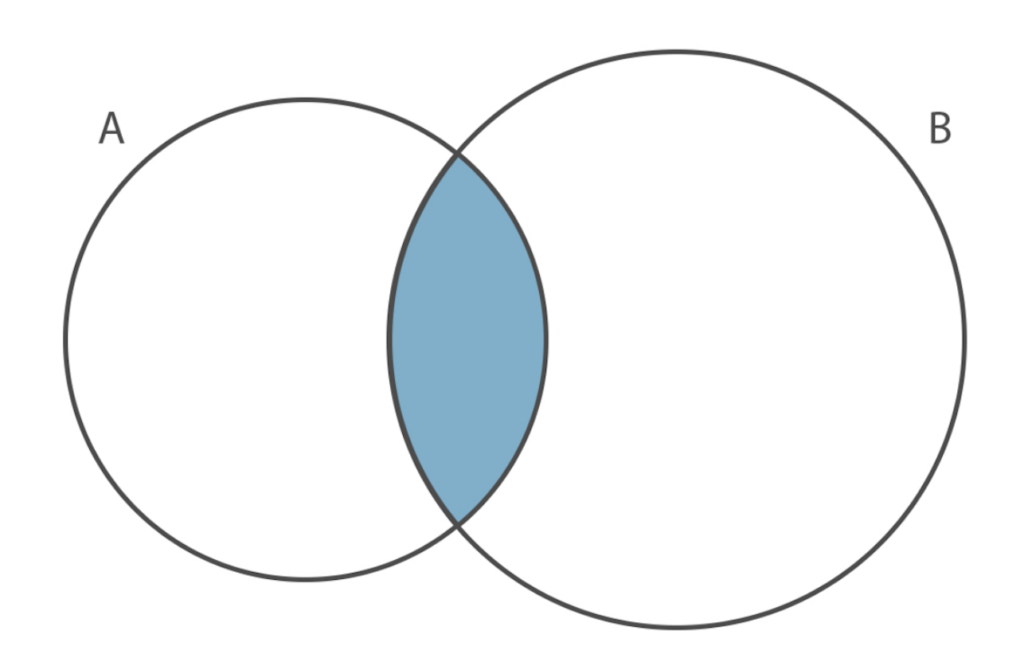
Intersezione di Insiemi
L’intersezione di due insiemi
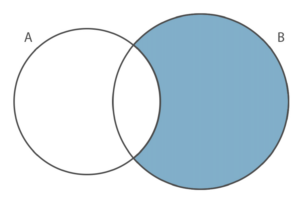
Differenza di Insiemi
La differenza B meno A si indica con
ed è data dall’insieme formato dai soli elementi di
Insiemi Coincidenti e Disgiunti
Due Insiemi A e B si dicono coincidenti se sono lo stesso insieme, cioè se e solo se hanno gli stessi elementi. Si dicono disgiunti se non hanno nessun elemento in comune.
Si dice che B è sottoinsieme di
Insieme Vuoto
Si chiama insieme vuoto I’insieme che non contiene nessun elemento. Tale insieme si indica con il simbolo
Q si utilizza per indicare i Numeri Razionali.
Esempi svolti
Siano
Rappresentare
Svolgimento
