Definizione di insieme
In matematica si usa la parola insieme per indicare una collezione di oggetti che sono detti elementi dell’insieme e che sono ben definiti e distinti tra loro.
Unione di Insiemi
L’unione di due insiemi $A$ e $B$ si indica con $A \cup B$ ed è l’insieme formato da tutti gli elementi di $A$ e $B$ presi una sola volta.
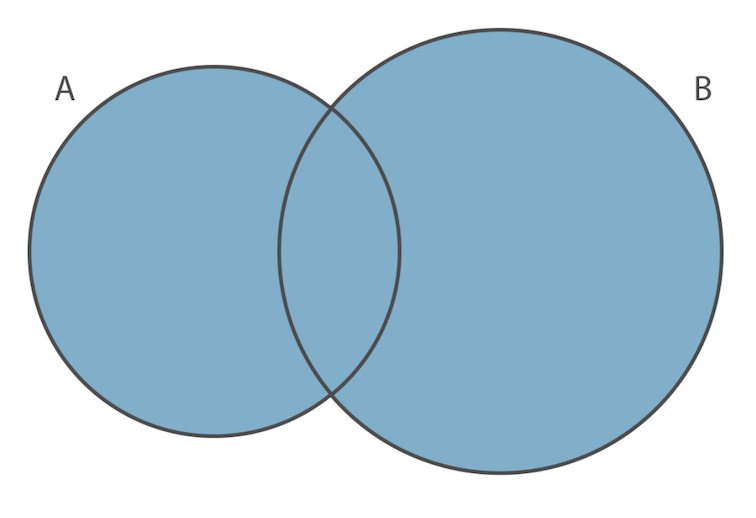
Intersezione di Insiemi
L’intersezione di due insiemi $A$ e $B$ si indica con $A \cap B$ ed è data dall’insieme formato da tutti gli elementi che appartengono sia all’insieme $A$ che all’insieme $B$ contemporaneamente.
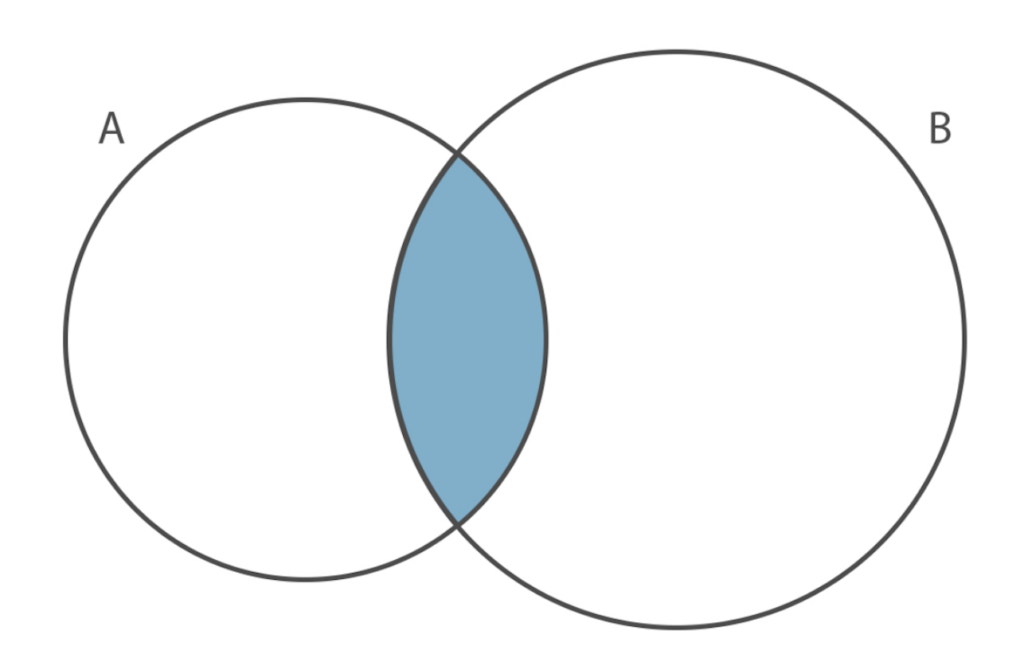
Differenza di Insiemi
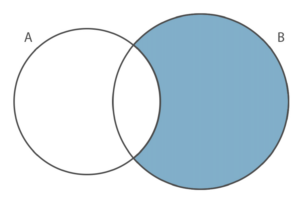
La differenza B meno A si indica con
$B \backslash \backslash A$ o con $ B – A$
ed è data dall’insieme formato dai soli elementi di $B$ che non appartengono ad A. B-A viene anche detto insieme complementare di $A$ in $B$.
Insiemi Coincidenti e Disgiunti
Due Insiemi A e B si dicono coincidenti se sono lo stesso insieme, cioè se e solo se hanno gli stessi elementi. Si dicono disgiunti se non hanno nessun elemento in comune.
Si dice che B è sottoinsieme di $A$ se $A$ contiene tutti gli elementi di $B$. Si indica nel seguente modo:
$$
B \subseteq A
$$
Insieme Vuoto
Si chiama insieme vuoto I’insieme che non contiene nessun elemento. Tale insieme si indica con il simbolo $\varnothing$ oppure con {} . L’insieme vuoto è sottoinsieme di qualsiasi altro insieme (incluso sé stesso).
$N$ si utilizza per indicare l’insieme dei Numeri Naturali.
$Z$ si utilizza per indicare i Numeri Interi Relativi.
Q si utilizza per indicare i Numeri Razionali.
Esempi svolti
Siano $A={2 ; 4 ; 6}, B={4 ; 7}, C={6 ; 4}$.
Rappresentare $(A \cap B) \cap C$ e $A \cap(B \cap C)$
Svolgimento
$$
A \cap B=(4) \quad B \cap C=(4)
$$
$$
\begin{gathered}
(A \cap B) \cap C=(4) \cap(6 ; 4) \
=(4)
\end{gathered}
$$
$$
\begin{aligned}
A \cap(B \cap C) &=(2 ; 4 ; 6) \cap(4) \
=&(4)
\end{aligned}
$$
$$
\begin{aligned}
A \cap(b \cap C) &=(2 ; 4 ; 6) \cap(4) \
=&(4)
\end{aligned}
$$
