Circonferenza Goniometrica
La circonferenza goniometrica è una particolare circonferenza avente il centro O coincidente con l’origine di un sistema di assi cartesiani
Tale circonferenza viene utilizzata per semplificare le definizioni delle funzioni goniometriche. Prendendo un punto qualsiasi A sulla circonferenza e tracciando una retta da quel punto al centro della circonferenza, otteniamo un triangolo rettangolo
Seno
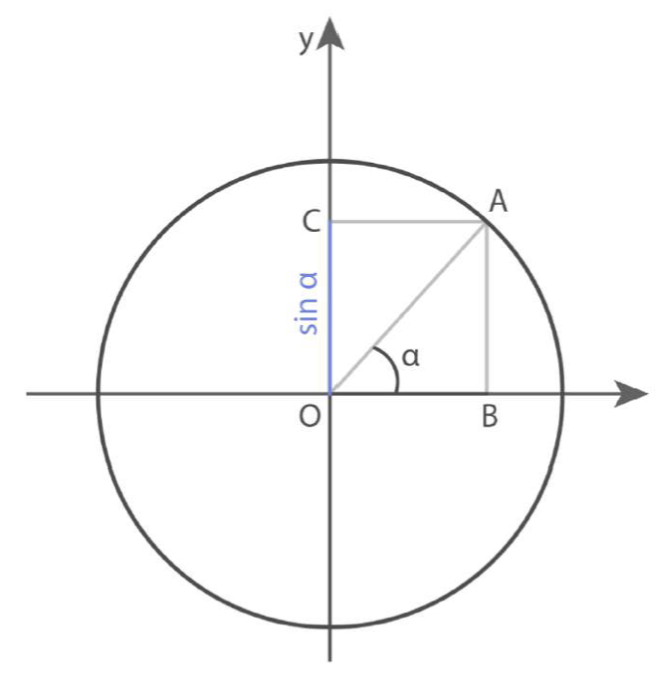
Il seno dell’angolo
Il seno di un angolo a è compreso tra – 1 e +1 .
Coseno
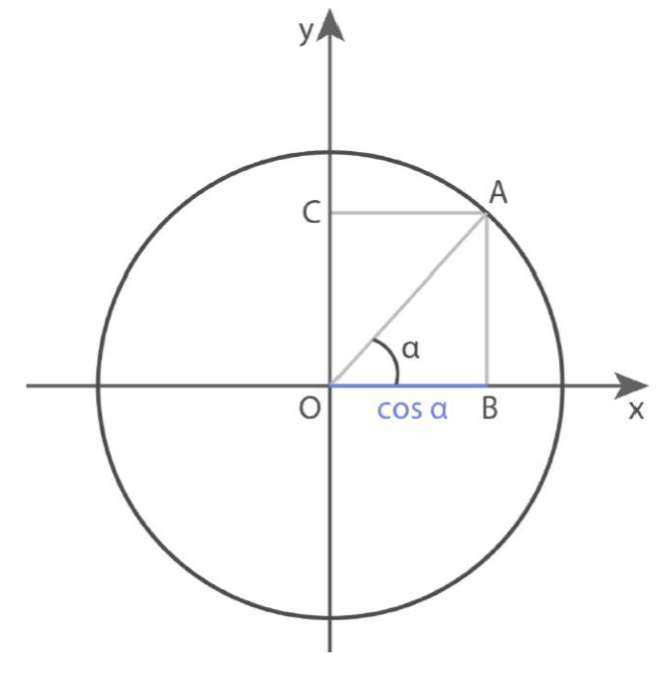
Il coseno dell’angolo a, indicato con la notazione cos a è il rapporto tra il cateto OB (adiacente all’angolo a) e l’ipotenusa
Il coseno di un angolo a è compreso tra – 1 e +1 .
Tangente
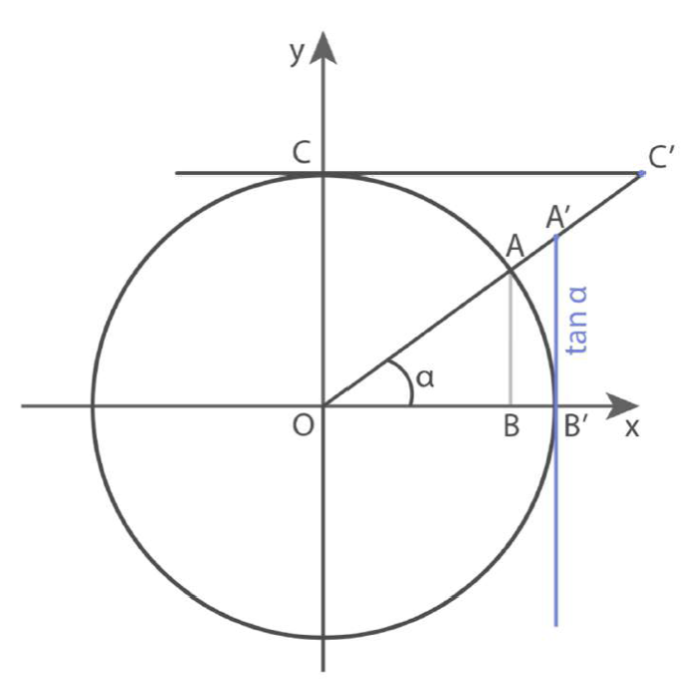
La tangente dell’angolo a, indicata con
Cotangente
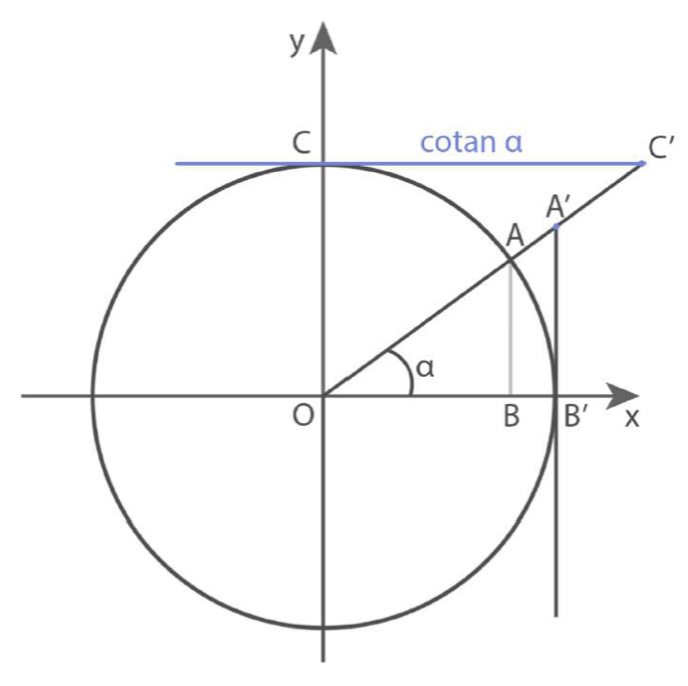
La cotangente dell’angolo a, indicata con cotan a è il rapporto tra il cateto
Relazione Fondamentale
La relazione
è nota come relazione fondamentale della goniometria e ci dice che la somma dei quadrati del seno e del coseno di uno stesso angolo sono sempre uguali all’unità.
