Definizione di Frazione
La frazione è un operatore che divide un intero in parti uguali e ne considera alcune di esse.
Esempi svolti
Esempio 1
Sommare
$$
\frac{1}{2}+\frac{1}{5}
$$
Svolgimento
La prima cosa da fare è quella di determinare un comune denominatore. In questo caso 10 rappresenta il comune denominatore per 2 e 5.
Adesso dobbiamo vedere come cambierà il numeratore di entrambe le frazioni. Moltiplichiamo il numeratore e il denominatore della prima frazione per 5 , mentre moltiplichiamo per 2 il numeratore e il denominatore della seconda frazione, come mostrato di seguito:
$$
\begin{array}{l}
\frac{1}{2} \cdot \frac{5}{5} \
\frac{1}{5} \cdot \frac{2}{2}
\end{array}
$$
Queste frazioni sono equivalente alle originali, ma con uguale denominatore. Adesso possiamo sommare i numeratori:
$$
\frac{5}{10}+\frac{2}{10}=\frac{5+2}{10}=\frac{7}{10}
$$
Esempio 2
Carolina ha preparato 24 torte di mele con una nuova ricetta. $1 / 3$ delle torte non è lievitato durante la cottura. Quante torte non sono lievitate?
Svolgimento
Tutto ciò che occorre fare è moltiplicare la frazione per il numero totale delle torte. Ricorda
$$
\frac{1}{3} \text { di } 24=\frac{1}{3} \cdot 24
$$
Quindi dividendo 3:3=1 al denominatore e 24:3=8 al numeratore si ha:
$$
\begin{array}{c}
\frac{1}{3} \cdot 24 \ =
\frac{1}{1} \cdot 8
\end{array}
$$
Soltanto 8 torte non sono lievitate.
Parti di una Frazione
Una frazione è composta da un numeratore e un denominatore. II numeratore indica quante parti sono state considerate. Il denominatore indica in quante parti è stato diviso l’intero.
$$
\frac{\text { numeratore }}{\text { denominatore }}
$$
Tipi di Frazioni
Esistono diverse tipologie di frazioni. Di seguito vediamo quali.
- Frazioni Proprie: sono le frazioni in cui il numeratore è più piccolo del denominatore.
$$
\frac{3}{4}
$$
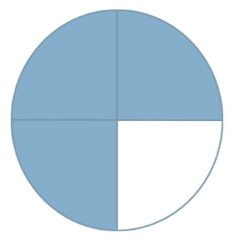
- Frazioni Improprie: sono le frazioni in cui il numeratore è maggiore del denominatore.
$$
\frac{11}{4}
$$
- Frazioni Apparenti: sono tutte quelle frazioni in cui il numeratore è multiplo del denominatore.
$$
\frac{12}{4}
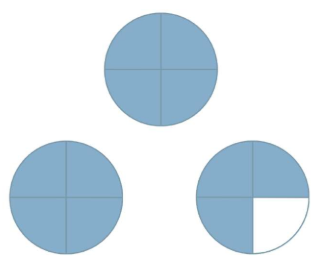
$$ - Frazioni Equivalenti: due o più frazioni si dicono equivalenti quando indicano la stessa quantità, anche se scritta in modo diverso.
Per esempio $1 / 2,2 / 4$ e $4 / 8$ sono tutte frazioni equivalenti.
- Numeri Misti: sono composti da un numero intero e una frazione.
$$
2 \frac{1}{2}=2+\frac{1}{2}
$$
Convertire un Numero Misto in Frazione Impropria
Per passare da un numero misto a una frazione impropria occorre seguire alcuni semplici passaggi.
Passaggio 1: Si moltiplica il denominatore della frazione per il numero intero.
Passaggio 2: Al prodotto ottenuto si aggiunge il numeratore della frazione.
Passaggio 3: Il denominatore della frazione impropria sarà lo stesso di quello presente nella frazione del numero misto.
$$
\begin{array}{r}
3 \frac{1}{4} \rightarrow \frac{(3 \cdot 4)+1}{4} \
=\frac{13}{4}
\end{array}
$$
Convertire una Frazione Impropria in Numero Misto
Occorre dividere il numeratore per il denominatore. Il risultato ottenuto sarà il numero intero del numero misto. Mentre il resto della divisione rappresenterà il numeratore della frazione. Il denominatore rimane sempre lo stesso.
$$ \frac{13}{6} =13 \div 6=2 \text { più resto } 1 $$
$$\frac{13}{6}=2 \frac{1}{6}$$
Somma e Differenza di Frazioni con Uguale Denominatore
La somma, o differenza, di più frazioni aventi lo stesso denominatore, è una nuova frazione in cui il numeratore è la somma, o differenza, dei numeratori e il denominatore è sempre lo stesso.
$$\frac{3}{7}+\frac{1}{7}=\frac{3+1}{7}=\frac{4}{7} $$
$$\frac{7}{13}-\frac{5}{13}=\frac{2}{13} $$
Somma e Differenza di Frazioni con Diverso Denominatore
Il primo passo da effettuare è quello di trovare lo stesso denominatore. Poi occorre sommare o sottrarre i numeratori.
Moltiplicazione di Frazioni
Moltiplicare due frazioni è un’operazione molto semplice. Basta moltiplicare tra di loro i numeratori e poi i denominatori. Se necessario, semplificare la frazione ottenuta.
$$
\frac{4}{3} \cdot \frac{2}{7}=\frac{8}{21}
$$
Moltiplicazione di una Frazione per un Numero Intero
Passaggio 1: Riscrivere il numero intero come una frazione, ciò significa scrivere 1 come denominatore.
Passaggio 2: Moltiplicare i numeratori.
Passaggio 3: Moltiplicare i denominatori ed eventualmente semplificare la frazione ottenuta.
$$
\frac{2}{3} \cdot 2 \rightarrow \frac{2}{3} \cdot \frac{2}{1}=\frac{4}{3}
$$
Moltiplicazione tra Numeri Misti
Passaggio 1: Convertire i numeri misti in frazioni improprie.
Passaggio 2: Moltiplicare i numeratori.
Passaggio 3: Moltiplicare i denominatori.
Passaggio 4: Se necessario, semplificare la frazione ottenuta.
Passaggio 5: Convertire il risultato in un numero misto.
$$
\begin{array}{c}
3 \frac{1}{2} \cdot 1 \frac{1}{4}=\frac{7}{2} \cdot \frac{5}{4} \
\frac{35}{8}=4 \frac{3}{8}
\end{array}
$$
Divisione tra Frazioni
Per eseguire la divisione tra due frazioni occorre invertire la seconda frazione ed eseguire la moltiplicazione.
$$\frac{3}{7} \div \frac{9}{4} $$
Dividendo 3:3=1 e 9:3=3 si ottiene:
$$\frac{1}{7} \cdot \frac{4}{3}=\frac{4}{21}$$
Divisione tra una Frazione e un Numero Misto
il primo passo da fare è quello di trasformare il numero intero in frazione, ponendo 1 come denominatore. Fatto ciò, occorre eseguire la moltiplicazione tra la prima frazione e l’inversa della seconda frazione.
$$ \frac{3}{2} \div 6 $$
$$\frac{3}{2} \div \frac{6}{1}$$
Dividendo 3:3=1 e 6:3=2 si ottiene
$$\frac{1}{2} \cdot \frac{1}{2}=\frac{1}{4}$$
